|
Rodzaj działania
|
zapis
|
Przykład i komentarz
|
| Dodawanie wektorów |
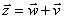
|
(2 + 3, 5 + (-7)) = (5, -2)
Dodajemy odpowiednie współrzędne.
Z = (5, -2)
|
| Odejmowanie wektorów |
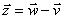
|
(2 - 3, 5 - (-7)) = (-1, 5 + 7) = (-1, 12)
Odejmujemy odpowiednie współrzędne.
Z = (-1, 12)
|
| mnożenie wektora przez liczbę |
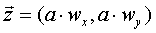
|
3 ∙ (2,5) = (6,15)
mnożymy przez liczbę, każdą ze współrzędnych wektora.
Z = (6,15)
|
| Mnożenie skalarne wektorów |
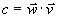
c = wx ∙ vx
+ wy∙ vy
|
(2,5) ∙ (3,-7) = 6+(-35)=-29
mnożymy przez siebie współrzędne obu wektorów, a otrzymane iloczyny
dodajemy
|
| mnożenie wektorowe wektorów |
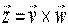
Wartość wektora Z można obliczyć ze wzoru:
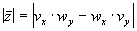
|
Wartość iloczynu wektorowego wektorów (2,5) i (3,-7)
|(2,5) x (3,-7)| = |-14 -15|=|-29|=29
Aby otrzymać wartość iloczynu wektorowego, mnożymy współrzędne
"na krzyż", otrzymane iloczyny odejmujemy i wyciągamy wartość
bezwzględną z wyniku.
|
| znajdowanie wartości wektora |
na płaszczyźnie: 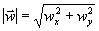
w przestrzeni: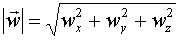
otrzymujemy skalar
|
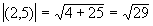
Podnosimy współrzędne do kwadratu, wyniki dodajemy, a otrzymaną sumę
pierwiastkujemy.
|
|

To jest obrazek dla urozmaicenia wyglądu podręcznika
|
Istnieje oczywiście wzór na wszystkie składowe iloczynu
wektorowego, ale posługuje się on najczęściej zaawansowanym matematycznie
pojęciem tensora (patrz krótkie wyjaśnienie)
i w licealnym (i tym bardziej gimnazjalnym) programie
fizyki nie jest on ani uwzględniony, ani wykorzystany.
Pełną tabelę,
łącznie ze wspomnianym wzorem, zamieszczę w ostatecznej CD - romowej
wersji Podręcznika. |