|
|
Graficzne dodawanie wektorów
|
||||||||
| reguła równoległoboku | |
| reguła trójkąta |
Reguła równoległoboku dodawania wektorów
Załóżmy, że początkowo mamy dwa różne wektory
- niebieski i czerwony:
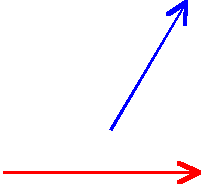
Za chwilę dodamy je graficznie omawiając kolejne etapy postępowania:
Etap 1: wektory zaczepiamy we wspólnym początku (kierunek, zwrot i długość obu wektorów nie mogą ulec zmianie). Trzeba przenieść (zachowując jego kierunek i zwrot) jeden z wektorów do początku drugiego
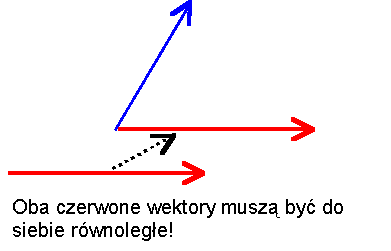
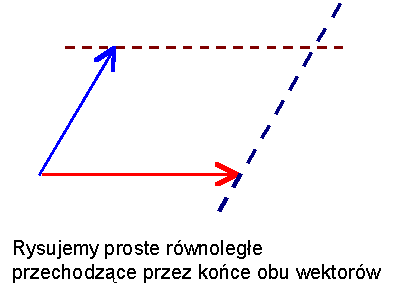
Etap 2: przez koniec pierwszego wektora prowadzimy prostą
równoległą do drugiego wektora, a następnie przez koniec drugiego
wektora prowadzimy równoległą do pierwszego wektora.
Etap 3 (kończący dzieło): wspólny początek wektorów (początek
wektora-sumy) łączymy z punktem przecięcia prostych z utworzonych na
etapie poprzednim (będzie to koniec wektora-sumy)

Reguła trójkąta dodawania wektorów
Załóżmy znowu, że, jak poprzednio, początkowo mamy dwa wektory:
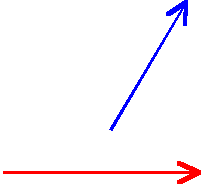
Aby dodać je metodą trójkąta posłużymy się następującą metodą:
Etap 1: początek jednego wektora zaczepiamy w końcu drugiego wektora. Musimy po prostu przenieść jeden wektor zachowując jego kierunek, zwrot i długość.
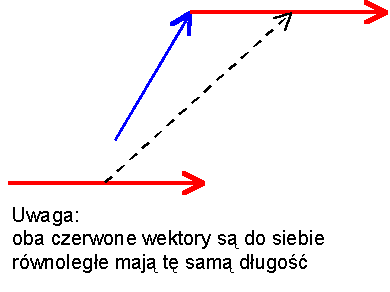
Etap 2: początek pierwszego wektora (będzie to początek wektora-sumy) łączymy z końcem drugiego wektora (będzie to koniec wektora-sumy).
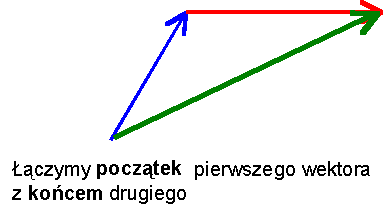
Gotowe! – wektor zielony jest sumą wektorów – niebieskiego i czerwonego
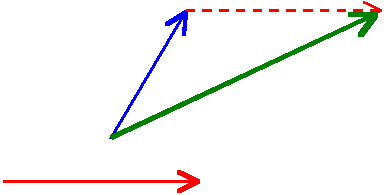
Dodawanie graficzne wektorów - przykłady:
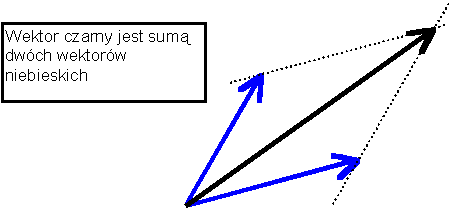

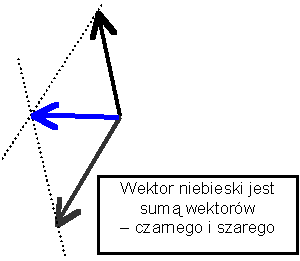

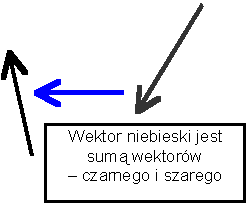
Dodawanie wektorów mających ten sam kierunek
W przypadku gdy oba wektory leżą na jednej prostej nie da się wykreślić równoległoboku ani (rozsądnie wyglądającego) trójkąta. Wtedy posługujemy się metodą zbliżoną zasadami do metody trójkąta, jednak nieco inaczej się prezentującą:
- Sytuacja początkowa – mamy dwa wektory o takim samym kierunku

- Przenosimy jeden wektor zaczepiając jego początek w końcu
drugiego wektora (tak jak w regule trójkąta).

- Wektor suma (na rysunku zielony) – ma początek w początku pierwszego, a koniec w końcu drugiego wektora:

Przypadek wektorów o przeciwnych zwrotach
Trochę inaczej wygląda dodawanie wektorów różniących się zwrotami.

Wtedy po przeniesieniu początku jednego wektora do końca drugiego, uzyskamy częściowe pokrywanie się strzałek obu tych wektorów.

Co nie zmienia sytuacji, że wektor – suma będzie miał początek w początku pierwszego, a koniec w końcu drugiego wektora:


Podsumowanie dodawania wektorów o tym samym kierunku
Można zauważyć, że dodawanie wektorów leżących na jednej prostej polega na:
|
sumowaniu ich długości gdy zwroty obu wektorów są zgodne | |
|
znajdowaniu różnicy długości gdy zwroty wektorów są przeciwne |