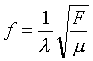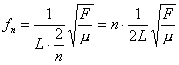Kojarząc ze sobą wzory na prędkość dźwięku w strunie oraz wzór na częstotliwość drgań fali dźwiękowej możemy dowiedzieć się od jakich wartości zależeć będzie wysokość wydobywanego przez strunę dźwięku:

F – siła naciągu struny (w układzie SI w niutonach N)
m - masa jednostki długości struny (w układzie SI w kg/m)
v - prędkość dźwięku w strunie (w układzie SI w m/s)
λ – długość fali wytworzonej w strunie (w układzie SI w metrach m)
f – częstotliwość tonu wytworzonego w strunie (w układzie SI w hercach
1 Hz =1/s)

Aby obliczyć stąd częstotliwość wydawanego przez strunę dźwięku należy zamiast długości fali wstawić odpowiednią wielkość dla pierwszej harmonicznej, czyli tonu podstawowego. W tym przypadku:

λ = 2 L

Dlatego częstotliwość dźwięku (częstotliwość tonu podstawowego) wydawanego przez strunę wyraża się wzorem:

Korzystając z tego wzoru, możemy ostatecznie wyliczyć od czego zależy wysokość dźwięku gitary, fortepianu czy skrzypiec:

	od długości efektywnej struny (efektywnej – bo można ją skracać np. przyciskając palcami do gryfu) – im krótsza jest struna tym większa będzie częstotliwość drgań (wyższy dźwięk).
	od siły naciągu struny - większa siła naciągu da większą częstotliwość wydobywanego dźwięku, czyli wyższy dźwięk
	od grubości struny i ciężaru materiału z jakiego ją wykonano – im grubsza (cięższa) struna, tym mniejsza częstotliwość, a więc i niższy dźwięk.

Struna, oprócz tonu podstawowego – najniższego wśród produkowanych tonów i decydującego o wysokości dźwięku – wydaje tony dodatkowe, czyli wyższe harmoniczne.

Możemy tu skorzystać ze wzoru (patrz rozdział Mody drgań struny - opis):

λ_n = L ∙ 2/n

Podstawiając wielkości λ_n do wzoru

Otrzymamy częstotliwości kolejnych harmonicznych. Będą one wielokrotnościami wyprowadzonej wyżej częstotliwości tonu podstawowego:

Podstawiając λ_n

Po podstawieniu n = 1 otrzymamy częstotliwość pierwszej harmonicznej (tonu podstawowego):

Podstawiając ten wzór do wzoru na f_n będziemy mieli:

f_n = n ∙ f₁

Czyli:

f₂ = 2 f₁f₃ = 3 f₁f₄ = 4 f₁

Tak więc kolejne harmoniczne mają częstotliwości będące wielokrotnościami częstotliwości tonu podstawowego.

Przykład:

Gdy częstotliwość tonu podstawowego (pierwsza harmoniczna) wynosi 110 Hz, to...
druga harmoniczna będzie miała częstotliwość: 220 Hz,
Ta harmoniczna nie zmienia wysokości dźwięku, lecz wzbogaca jego barwę.
Trzecia harmoniczna: 330 Hz.
Ta harmoniczna nie zmienia wysokości dźwięku, lecz wzbogaca jego barwę.
Czwarta harmoniczna - 440 Hz...
itd....

wzór na częstotliwość fali dźwiękowej << Częstotliwość dźwięku wytwarzanego przez strunę