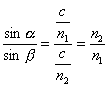|
Stąd ostatecznie będziemy mieli drugą postać prawa załamania
światła.
Wzór prawa załamania – postać 2
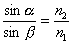
Ta wersja prawa załamania wiąże kąty padania i załamania z
bezwzględnymi współczynnikami załamania w obu ośrodkach.
Sformułowanie słowne:
Stosunek sinusa kąta
padania, do sinusa kąta załamania jest równy stosunkowi bezwzględnego
współczynnika załamania ośrodka do którego przechodzi fala,
do bezwzględnego współczynnika załamania ośrodka, z którego
fala pada na powierzchnię rozgraniczającą oba ośrodki.
Wzór prawa załamania – postać 3
Jest jeszcze trzecia postać prawa załamania. Powstaje ona po
zdefiniowaniu kolejnej wielkości zwanej względnym współczynnikiem
załamania:
|
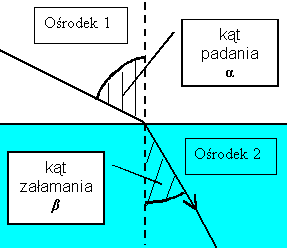
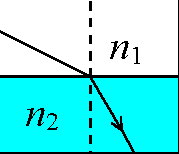 Podstawimy
ten wzór raz w wersji dla ośrodka 1
Podstawimy
ten wzór raz w wersji dla ośrodka 1