Inne

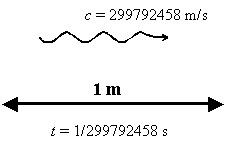
Długość

"Długość", "odległość", "odstęp" - to nazwy na tę samą wielkość fizyczną, będącą podstawową jednostką sytuującą punkty w przestrzeni.

Ścisłe definiowanie odległości jest domeną matematyki i oparte jest o pewien zestaw podstawowych postulatów definiującą dany typ przestrzeni. Dla fizyków najważniejsza jest oczywiście przestrzeń nas otaczająca, czyli przestrzeń w której usytuowane są otaczające nas obiekty i w której zachodzą różne zdarzenia.

Jednostka długości

Standardowo długość (w układzie SI) mierzymy ją w metrach i oznaczam literą małe „em” - m.

Skąd się wzięła ta jednostka?

Początkowo został on zdefiniowany jako 1/10 000 część ćwiartki ziemskiego południka (dlatego obwód Ziemi jest dziś równy dość dokładnie 40 000 km), później zdecydowano się na wzorzec związany z długością platyno – irydowej szyny zamkniętej w Sevres pod Paryżem (iryd – pierwiastek metaliczny – element stopu, z którego wykonano wzorzec - patrz też jednostki układu SI), a od lat 80-tych XX wieku metr wynika z odległości jaką przebywa światło w próżni.

Aktualnie metr definiuje się jako:

Definicja metra

1 metr jest równy drodze jaka przebywa w próżni światło w ciągu czasu 1/299792458 sekundy.

W razie potrzeby (wygody) jednak długość można wyrażać w jednostkach wielokrotnych, lub podwielokrotnych związanych z tą jednostką.

Jednostki pochodne metra np.:

1 pm = 10^-12 m
1 nm = 10^-9 m
1 mm = 0,001 m = 10^-3 m
1 cm = 0,01 m
1 km = 1000 m

Póki co, nie używa się jednostek pochodnych typu "gigametr", czy "megametr". Jednak zastosowanie takich terminów nie byłoby błędem, a co najwyżej pewną niezręcznością.

Inne jednostki odległości

W niektórych krajach świata do pomiaru odległości stosuje się inne niż metr jednostki.

1 mila angielska = 1,609 km
1 mila morska = 1,852276 km
1 yard = 0,9144 m
1 cal = 25,4 mm
1 stopa angielska: 1 ft = 12 cali = 30,48 cm
1 jednostka astronomiczna (AU). 1 AU = 1,4959789 ∙ 10¹¹ m
i inne.

W astronomii najczęściej stosuje się jednostki oparte nie o metr, ale o czas w jakim światło przebywa drogę:

rok świetlny - jest to odległość jaka światło przebywa w ciągu roku.
1R.ś. = 63240 AU = 9,4605 ∙ 10¹⁵ m

Alternatywnym sposobem jest oparcie długości na pomiarze kąta pod jakim widziany byłby odcinek.

parsek (pc, dawniej ps) - jest to odległość z której odcinek równy jednostce astronomicznej byłby widziany pod kątem jednej sekundy łuku (1"). Inaczej mówiąc gdyby ktoś z odległości parseka patrzył na nasz Układ Słoneczny, to odległość od Ziemi do Słońca widziana byłaby jako właśnie (1"). Pod takim katem 1 mm jest widziany z odległości ok. 1,3 km.
1 pc = 206265 AU = 3,26 lat świetlnych = 3,094 ∙ 10¹⁶ m

Typowa odległość między układami gwiazdowymi w obszarze Galaktyki sąsiadującym z Układem Słonecznym jest właśnie rzędu parseków - np. najbliższa odległość do gwiazdy innej niż Słońce (Proxima Centauri) jest równa ok. 1,3 pc.

jednostka astronomiczna (AU, j.a.) - wielkość równa średniej odległości od Ziemi do Słońca. Bardziej ściśle określa się ją jako długość wielkiej półosi orbity Ziemi wokół Słońca.
1 AU = 1,4959789 ∙ 10¹¹ m.

Warto (i łatwo jest) zapamiętać, że 1 AU to ok 150 mln km.

Symbole odległości we wzorach

We wzorach odległość oznaczana jest na kilka sposobów. Najczęściej autorzy posługują się literą „el” – L, l (el duże i el małe), co pochodzi od angielskiego terminu length oznaczającego właśnie odległość. Konkurencyjne oznaczenie to d – zwyczajowo stosowane do określania średnicy, choć nie tylko... (ang. diameter – średnica, lub distance - odległość). W kinematyce z kolei przyjęło się odległość nazywać „drogą” i oznaczać przez S. To oznaczenie pochodzi zapewne od angielskiej nazwy odcinka (ang. sector – odcinek, także w znaczeniu odległości). W razie potrzeby dla oznaczania odległości, drogi używane się również inne litery alfabetu – najczęściej: a, b, c, z, y, z.

Aby podkreślić, że odległość jest różnicą położenia między punktem początkowym i końcowym stosuje się oznaczenie odległości za pomocą „delty”:

∆L , ∆S , ∆x

Właściwie użycie delty niewiele wnosi do interpretacji równań - cały czas mamy do czynienia z odległością. Znaczenie tego sposobu zapisu rośnie gdy przechodzimy do różniczkowych (czyli wynikającej z wyższej matematyki) postaci wzorów.

Inne informacje

O pomiarach odległości można przeczytać w rozdziale Pomiary odległości.