Nacisk, ciśnienie

Tematy uzupełniające
Normalna do powierzchni

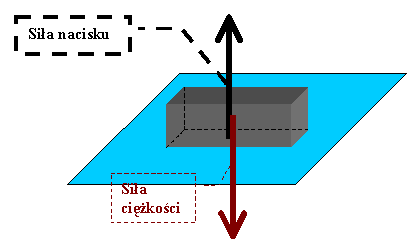
Co warto wiedzieć wcześniej?
siła, prędkość, wektory i skalary, siła ciężkości

Przykłady sił nacisku

Siłę nacisku oblicza się na różne sposoby w zależności od sytuacji. Podam tutaj kilka często spotykanych przypadków.

Nacisk na klocek spoczywający na poziomej powierzchni

Jeżeli jakieś ciało położymy na poziomej powierzchni, to będzie ona swoim naciskiem na to ciało (skierowanym do góry!), podtrzymywać je przeciwstawiając się spadaniu.

W takiej sytuacji:

Siła nacisku powierzchni na ciało zrównoważy siłę ciężkości.
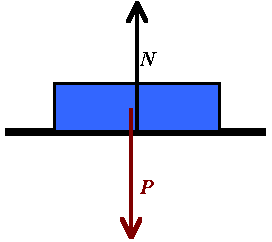
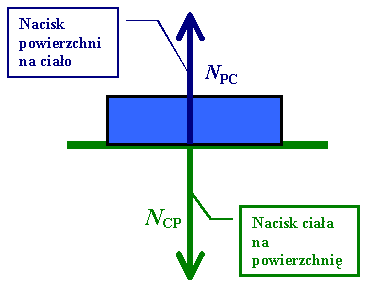
(wyjątkiem byłaby sytuacja, w której powierzchnia porusza się z przyspieszeniem w górę lub w dół)

Przyjrzyjmy się teraz dokładniej siłom działającym na leżące ciało:

Obliczymy wartość siły nacisku przy założeniu, że ciało ma masę m.
Najpierw narysujmy powyższą sytuację schematycznie i z zastosowaniem oznaczeń

	N – siła nacisku
	P – siła ciężkości.

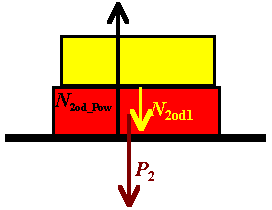
Warto zauważyć, że:
Siły nacisku i ciężkości równoważą się ponieważ działają na to samo ciało, mają takie same wartości i kierunki ale przeciwne zwroty.

Uwaga na częsty błąd! - kiedy siły się równoważą, a kiedy nie?...

Podkreślam tu fakt, że siły „działają na to samo ciało”. Niestety, dość często popełniany jest błąd mylenia siły ciężkości z siłą nacisku. Wynika on prawdopodobnie z faktu, że np. w powyższej sytuacji mamy aż dwie siły nacisku, a wartość obu jest taka sama jak wartość siły ciężkości.

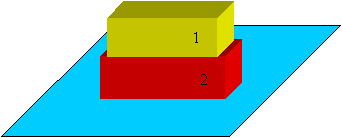
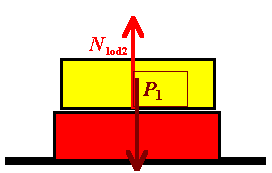
Oto przykład sytuacji, w której mają równe wartości i przeciwne zwroty, lecz nie równoważą się:

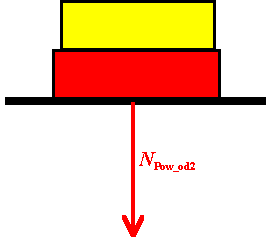
	Nacisk powierzchni na ciało - podtrzymujący to ciało przed upadkiem (skierowany do góry)
	Nacisk ciała na powierzchnię pod nią – przyciskający ją (skierowany w dół)

Ale, ponieważ siły te działają na różne ciała, więc nie mogą się równoważyć się i nie można ich ze sobą sumować, ani odejmować od siebie.

Powróćmy jednak do sił działających na nasze ciało – mamy ich w tej sytuacji dwie:

siłę ciężkości ciągnącą ciało w dół

siłę nacisku podtrzymującą ciało przed upadkiem. W tym przypadku siła ta nazywana jest często siłą reakcji podłoża.

Siły te równoważą się, dzięki czemu klocek nie spada, ani nie wznosi się do góry.

Wartości tych sił są równe:

Jeśli oznaczymy: N - wartość siły nacisku, a P - wartości siły ciężkości.

To z faktu, że P = m·g, wyniknie nam także:

N = m·g.

Uwaga końcowa:

Powyższe rozważania odnoszą się nie tylko do klocka spoczywającego na poziomej powierzchni, ale także do sunącego po niej bez tarcia (gdyby było tarcie, na rysunku pojawiłaby się jeszcze jedna siła).

Przykład 2 - dwa klocki umieszczone jeden na drugim

Ciekawym przypadkiem dobrze obrazującym czym zjawisku nacisku, jest problem dwóch klocków, umieszczonych na poziomej powierzchni jeden na drugim.

Załóżmy, że

	górny klocek (oznaczmy go numerem 1) ma masę m₁
	klocek dolny (numer 2) masę m₂.

Obliczymy wszystkie siły działające na każde z trzech ciał – obydwa klocki i powierzchnię pod nimi.

Klocek 1

Najpierw weźmiemy się za górny klocek – tutaj sytuacja jest identyczna jak w problemie rozważanym poprzednio. Dlatego już bez zbytnich dywagacji napiszemy:

Na klocek 1 działają dwie siły:

	Siła ciężkości o wartości P₁ = m₁·g skierowana w dół
	Siła nacisku od klocka dolnego. Siła ta jest skierowana do góry i musi zrównoważyć ciężar 1. Jej wartość: N_1od2 = m₁·g

Powyższe siły się równoważą (wartości obu sił są równe), więc klocek nie porusza się.

Klocek 2

Teraz rozważymy siły działające na klocek 2 (czerwony). Działają tu trzy siły:

Siła ciężkości P₂ tego klocka (skierowana w dół)
Siła nacisku pochodząca od klocka 1, czyli N_2od1 (skierowana w dół)
Siła nacisku pochodząca od dolnej powierzchni, czyli N_{2od_Pow} (skierowana w górę)

Wartości tych sił są następujące:

Siła ciężkości P₂ = m₂· g
Siła nacisku od klocka 1 (górnego) jest równa co do wartości sile, jaką klocek 2 działa na klocek 1 – wynika to z III zasady dynamiki Newtona. Można więc napisać:
N_2od1 = N_1od2 = m₁·g
Siła nacisku powierzchni na klocek 2 musi zrównoważyć ciężar obu znajdujących się nad nią ciał, czyli jest sumą obu tych sił ciężkości:
N_{2od_Pow} = P₁ + P₂ = m₁·g + m₂·g=( m₁ + m₂)·g.

Oczywiście siła nacisku od powierzchni (skierowana do góry) równoważy obie siły działające w dół. Dzięki temu powyższy klocek też pozostaje w równowadze.

N_{2od_Pow} = N_2od1 + P₂

Siły działające na powierzchnię

Na powierzchnię działa od góry nacisk pochodzący od klocka 2. Jego wartość jest równa ciężarowi obu klocków: 1 i 2

N_{Pow_od2} = P₁ + P₂ = m₁·g + m₂·g

Wyciągamy g przed nawias:

N_{Pow_od2}=( m₁ + m₂)·g

Wnikliwy czytelnik zapewne zauważy:

to jak to... działa tylko jedna siła? – przecież pod jej wpływem powierzchnia powinna przyspieszać w dół?...

- no cóż, słuszna uwaga. Musi więc istnieć jakaś dodatkowa, nieznana siła, która z kolei tę powierzchnię utrzymuje w równowadze. Ta ukryta siła równoważy zarówno siłę nacisku od klocka 2, jak też ciężar materiału, z którego wykonano powierzchnię. Ale tą ostatnią siłą nie będziemy już się zajmować.

Ciało na równi (pochylni)

Przypadek siły nacisku działającej na ciało umieszczone na pochyłej powierzchni rozpatrzono w dziale równia pochyła. Zwracam uwagę, że w opisie tego zadania siła nacisku równi na klocek (skierowana ukośnie do góry) nazwana została siłą reakcji podłoża (ew. patrz rozkład sił na równi pochyłej). Nie zmienia to jednak istoty sprawy, że jest to także siła nacisku, tylko inaczej oznaczona. Na równi dalej więc obowiązuje zasada, że siła reakcji - nacisku działa prostopadle do powierzchni, a powierzchnią na jakiej spoczywa klocek jest równia.