|
Równia - wstęp |
Równia - co to jest |
Równia - podstawowy problem |
Siły na równi |
Rysowanie sił |
Rozkład siły ciężkości |
Rysowanie siły reakcji równi |
Rysowanie siły tarcia |
Obliczanie siły wypadkowej |
Wyrażanie wartości sił składowych przez funkcje trygonometryczne |
Wzór końcowy na przyspieszenie klocka |
Klocek na równi - zadania dodatkowe |
Równia - rozwiązanie problemu 1 |
Rozwiązanie problemu 2
|
Co to jest równia pochyła?
 Na początek musimy
wyjaśnić sobie znaczenie pewnych używanych dalej terminów. Na początek musimy
wyjaśnić sobie znaczenie pewnych używanych dalej terminów.
- Dowolna płaszczyzna nachylona pod pewnym kątem do poziomu
może być uznana za równię pochyłą (nazywaną też
„pochylnią”).
Taką równią może być więc pozioma deska, powierzchnia okładki
książki, nawet szersza linijka. Ważne jest tylko, aby powierzchnia równi
się nie wyginała i aby jej chropowatość była jednolita na całej długości.
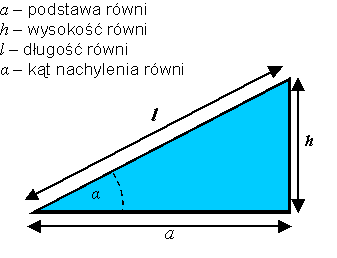
- Kąt pod jakim równia jest ustawiona w stosunku
do poziomu nazywamy kątem nachylenia równi i oznaczamy
zazwyczaj literami alfabetu greckiego α.(
niekiedy β)
- Określenie (używane w zadaniach), ze równia jest "gładka"
oznaczać będzie, że możemy zaniedbać siłę tarcia jaka występuje
pomiędzy klockiem, a równią
- Długość równi, jest to długość jaką przebywa klocek
wzdłuż równi, czyli jeśli startuje on z samej góry, będzie to
najdłuższy bok trójkąta jaki tworzy równia.
- Podstawa równi to poziomy bok trójkąta tworzącego równię.
- Wysokość równi, to trzeci - pionowy - bok trójkąta
tworzącego równię.
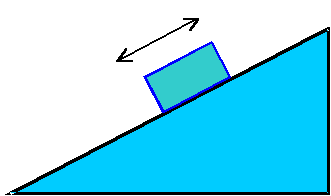 Oczywiście sama równia
to jeszcze nie wszystko co potrzebujemy. Na równi kładziemy klocek
(lub inny podobny przedmiot), który może się wzdłuż niej poruszać
– może się zsuwać, ale też (jeżeli zostanie początkowo pchnięty
do góry) dzięki nadanej początkowo prędkości może wjeżdżać na równię. Oczywiście sama równia
to jeszcze nie wszystko co potrzebujemy. Na równi kładziemy klocek
(lub inny podobny przedmiot), który może się wzdłuż niej poruszać
– może się zsuwać, ale też (jeżeli zostanie początkowo pchnięty
do góry) dzięki nadanej początkowo prędkości może wjeżdżać na równię.
Klocek też powinien mieć w miarę jednorodną powierzchnię. Może
to być klocek z drewna, piórnik, gumka itp.
|
 Na początek musimy
wyjaśnić sobie znaczenie pewnych używanych dalej terminów.
Na początek musimy
wyjaśnić sobie znaczenie pewnych używanych dalej terminów.
 Oczywiście sama równia
to jeszcze nie wszystko co potrzebujemy. Na równi kładziemy klocek
(lub inny podobny przedmiot), który może się wzdłuż niej poruszać
– może się zsuwać, ale też (jeżeli zostanie początkowo pchnięty
do góry) dzięki nadanej początkowo prędkości może wjeżdżać na równię.
Oczywiście sama równia
to jeszcze nie wszystko co potrzebujemy. Na równi kładziemy klocek
(lub inny podobny przedmiot), który może się wzdłuż niej poruszać
– może się zsuwać, ale też (jeżeli zostanie początkowo pchnięty
do góry) dzięki nadanej początkowo prędkości może wjeżdżać na równię.