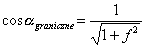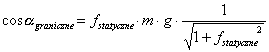Równia - rozwiązanie problemu 1

Rozwiązanie problemu 1:

Treść problemy jest opisana w rozdziale Klocek na równi - zadania dodatkowe.

Najpierw musimy uwiadomić sobie co powoduje ruch klocka. Wiadomo, dla małych kątów nachylenia klocek będzie wystarczająco przytrzymywany przez tarcie; dla dużych, klocek zsunie się.

Pojawia się zatem pytanie:
Przy jakim kącie nachylenia postawiony klocek zaczyna zsuwać się z równi?

Ten przypadek graniczny jest wynikiem zmiany w konfiguracji dwóch sił: siły ściągającej - działającej w dół i siły tarcia przytrzymującej. Wraz ze wzrostem kąta nachylenia równi zwiększa się wartość siły ściągającej. A co się dzieje z siłą tarcia?

- póki klocek spoczywa, musi istnieć równowaga tych sił (I zasada dynamiki Newtona), a więc siła tarcia musi rosnąć równoważąc siłę ciągającą. Jednak... tylko do pewnego momentu.

Do jakiego momentu? - do sytuacji, w której spełniony zostanie wzór:

Tutaj widzimy kolejny problem: to jak to... to do tej pory ten wzór nie obowiązywał (przecież jest podawany "jak prawdziwy"... - to po co się go uczymy?)

Ano właśnie! - powyższy wzór opisuje albo:

	wartość maksymalnej siły tarcia przy ruszaniu (tzw. tarcie statyczne), albo
	siły tarcia dynamicznego (dla klocka w ruchu).

Póki klocek spoczywa, ale nie ma tendencji do ruszania, dopóty siła tarcia wyrównuje się (zawsze nadążąjąc) do wartości siły ściągającej i wzór nie ma zastosowania.

Czyli mamy pierwszą część odpowiedzi:

Rozwiązanie - przypadek statyczny

Dla nieruchomego klocka siła tarcia jest równa sile ściągającej:

T = P_|| = P ∙ sin α

a ponieważ P = m ∙ g

T = m ∙ g ∙ sin α

Przypadek dynamiczny

Dopiero dla ruchomego klocka zaczyna obowiązywać wzór ze współczynnikiem tarcia. Wzór ten wyprowadzony został w rozdziale Wzór końcowy na przyspieszenie klocka. Jak można z niego wyczytać wartość siły tarcie wynosi wtedy:

T= f ∙ P ∙ cos α

czyli z racji na fakt, że P = m ∙ g

T= f ∙ m ∙ g ∙ cos α

Przypadek graniczny

Zajmijmy się teraz przypadkiem granicznym, czyli sytuacją, w której klocek rusza z miejsca. Wtedy stosujemy wzór na tarcie statyczne:

Oraz

T = P_||

Z pierwszego równania po pomnożeniu obu stron przez N otrzymamy:

T = f ∙N, czyli P_||=f ∙ N

Ale ponieważ

P_|| = P ∙ sin α , a N = P₊= P ∙cos α (patrz w rozwiązaniu głównego zadania), więc

P sin α = P ∙f ∙ cos α

Po podzieleniu obu stron równania przez P ∙cos a mamy:

,

ale z funkcji trygonometrycznych wiadomo, że

, czyli

tg α = f

I to jest szukana zależność dla kąta granicznego

tg α _graniczne _graniczne = f_statyczne

Siła tarcia dla kąta granicznego

A teraz obliczymy siłę tarcia dla kąta granicznego, przy założeniu że klocek jeszcze się nie poruszył. Dlatego obowiązuje dla niego wartość współczynnika tarcia statycznego..

Ponieważ:

T = f_statyczne N

Zaś (patrz główne rozwiązanie):

N = P ∙ cos α = m ∙ g ∙ cos α

więc:

T_graniczne = f_statyczne ∙ m ∙ g ∙ cos a _graniczne

Tutaj, aby być w pełni porządnymi należałoby jeszcze ów kosinus kąta wyrazić przez wartości dane, czyli przez f. Trzeba tu skorzystać z zależności trygonometrycznej

(patrz Wzory trygonometryczne)

tutaj znak jest oczywiście +, bo mamy do czynienia z kątem mniejszym niż 90°.

Ale skoro tg a _graniczne= f , to

I ostatecznie:

Wartości liczbowe

Podsumujmy nasze rozważania uszczegóławiając je dla wartości liczbowych podanych w zadaniu:

Jeżeli chcemy, aby klocek nie zsuwał się po równi o współczynniku tarcia statycznego 0,5 tangens kąta nachylenia równi musi spełniać warunek:

tg α _graniczne < 0,5

Zachodzi to dla kąta:

α _graniczne < 26,5°