|
Równia - wstęp |
|
Rozwiązanie problemu 2Jak to opisano w rozdziale Klocek na równi - zadania dodatkowe dane do zadania są następujące:
Tutaj siły tarcia nie ma Z rysunku widać, że:Siła ciężkości jest jak poprzednio częściowo równoważona przez siłę reakcji (dokładniej siła reakcji równoważy składową siły ciężkości prostopadłą do równi). Składowa siły ciężkości równoległa do równi (siła ściągająca) ma swoją oponentkę w postaci siły ciągnącej F. Jak wielka musi być F, aby pociągnąć klocek do góry?
Tak, ale o ile większa? - wystarczy, aby siła ta choćby na chwilę była minimalnie większa od składowej ściągającej (nawet np. o jedną bilionową Newtona). Wtedy klocek zostanie już ruszony i dalej można już tylko podtrzymywać jego prędkość działając siłą dokładnie równą sile ściągającej. Tak więc praktycznie przez prawie cały ruch ciągnąca siła może być równa sile ściągającej.
Ponieważ
więc (odpowiedź w zadaniu)
Podstawiamy dane:
A jaką siłą trzeba działać aby zwyczajnie podnieć klocek do góry? - zastosujemy wzór na siłę ciężkości:
Stosunek tych sił wynosi 0,5 - dwa razy łatwiej jest ciągnąć ciało po takiej równi, niż podnosić je. Pytanie dla czytelnika:A przy jakim współczynniku tarcia nie mielibyśmy żadnego zysku na sile, tzn. kiedy cały zysk z zastosowania równi zostałby wykorzystany na pokonanie siły tarcia? Odp.
|
||||||||||
|
...Rozw. problemu 1 | Rozwiązanie problemu 2 |
|
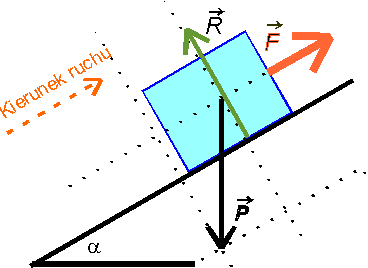 Zróbmy
rysunek, na którym zaznaczymy wszystkie działające siły:
Zróbmy
rysunek, na którym zaznaczymy wszystkie działające siły: