|
|
Zasada zachowania energii mechanicznejPojęcie energii mechanicznej jest niezwykle ważne z jednego powodu - w wielu sytuacjach, mimo zmiany różnych parametrów ruchu, sama energia nie zmienia się. Kiedy energia mechaniczna jest stała?W przypadku ruchu ciał w polu grawitacyjnym bez tarcia. Ciało może lecieć, ślizgać się, spadać itp. Jednak nie może występować tarcie, lub inne sytuacje, w których energia mechaniczna ulega zmianom (np. oddawanie energii za pomocą sił elektrycznych, czy magnetycznych. Sformułowanie 1 zasady zachowania energii mechanicznejW dowolnym ruchu przebiegającym bez tarcia (i innych strat energii) energia mechaniczna układu izolowanego jest stała.
Jeśli przyjrzymy się wzorowi na energię mechaniczną:
To ze stałości energii mechanicznej wyniknie nam, że:
Dlaczego tak się dzieje?Jeśli przyjrzymy się wzorowi:
to pewnie bez trudu zorientujemy się, że stałość sumy można zachować, jeśli ubytek jednego składnika jest natychmiast zrównoważony przyrostem drugiego składnika. Jeżeli więc podczas ruchu ubywa 5 J energii kinetycznej, to musi przybyć dokładnie 5 J energii potencjalnej (lub na odwrót).
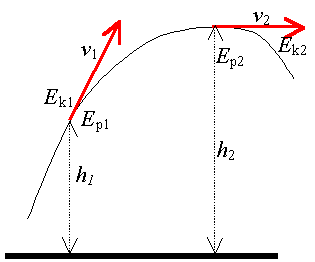
W sytuacji na rysunku:
Inne możliwe sformułowania zasady zachowania energii mechanicznejSformułowanie 2: Sformułowanie 3: Sformułowanie 4: Można to zapisać wzoramiEmech_układu_izolowanego = const, lub
lub Ekinet_1 + Epotencj_1 = Ekinet_2 + Epotencj_2
|
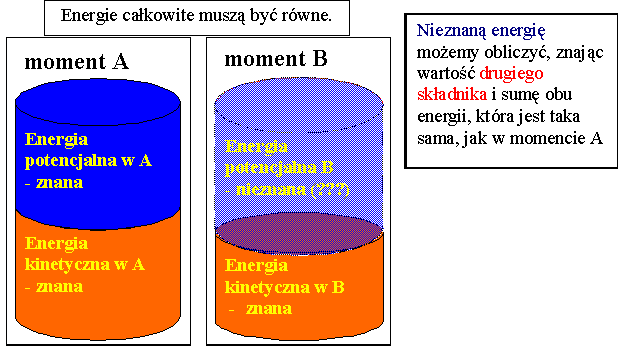
Co wynika praktycznie z zasady zachowania energii?Teraz wyjaśnimy co z powyższych sformułowań wynika. Załóżmy, że rozpatrywany przez nas układ posiada tylko dwa rodzaje energii: energię kinetyczną i potencjalną. Wtedy, z faktu, że wzrosła energia kinetyczna, możemy od razu wywnioskować o zmaleniu energii potencjalnej - bo suma tych dwóch składników musi być stała. I w ten sposób zazwyczaj stosuje się w zadaniach zasadę zachowania energii - jeśli znamy całkowitą energią w pewnym momencie, a następnie tylko jeden ze składników w innym momencie, to możemy obliczyć wartość tego brakującego składnika.
|
|