Definicja pracy - wektorowo

Energia

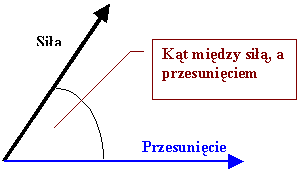
Jak to napisano w rozdziale poświęconym podstawom definicji pracy, rzeczywista wartość pracy zależy od wartości działającej siły, przesunięcia, a także kąta jaki tworzy ta siła z przesunięciem.

Wartość pracy, z uwzględnieniem kąta między siłą i przesunięciem, można też obliczyć ze wzoru:

W = F · S · cos (kąta między wektorem siły, a wektorem przesunięcia)

(powyższa procedura mnożenia wartości wektorów i kosinusa kąta między nimi jest określana jako mnożenie skalarne wektorów).

Wzór ten powstaje z wzorów podanych wcześniej dzięki zastąpieniu składowej siły w kierunku przesunięcia:

^{Siła_w_kierunku_przesunięcia = Wartość_całej_siły
· kosinus_kąta}

lub odpowiednio:

^{Przesunięcie_w kierunku_siły = Całe_przesunięcie
· kosinus_kąta}

(kosinus_kąta odnosi się do kąta pomiędzy siłą, a przesunięciem).

Praca jako iloczyn skalarny wektorów siły i przesunięcia

Powyższy zapis: W = F · S · cos (kąta między wektorem siły, a wektorem przesunięcia) - odpowiada dokładnie definicji iloczynu skalarnego dwóch wektorów.

Wnioskować z tego można, że zwięźlej da się zapisać definicję pracy w notacji wektorowej:

Ten zapis to nic innego, tylko zwięzłe zapisanie faktu, że wartość pracy jest iloczynem wartości wektorów siły i przesunięcia oraz kosinusa kąta między tymi wektorami.