|
|
Energia potencjalna ciężkościJak to opisano w rozdziale dotyczącym związku między pracą i energią, można przyjąć, że praca włożona w wyniesienie wody jest równa pracy jaką można odzyskać dzięki uderzeniom wody o łopatki młyna. Ten fakt, można nazwać jeszcze innymi słowami - mówimy, że woda zgromadzona na pewnej wysokości, posiada energię potencjalną ciężkości. Słowo „potencjalna” oznacza tu, że jest ona związana z położeniem i oddziaływaniem, czyli jest jakby energią statyczną, nie związaną z ruchem. Rodzajów energii potencjalnych jest kilka, a różnią się one typem oddziaływania, z którym są związane - oprócz energii potencjalnej ciężkości mamy jeszcze energię potencjalną sprężystości (związaną z oddziaływaniami sprężystymi) oraz energię potencjalną elektrostatyczną (m.in. działającą na cząstki naładowane poruszające się w polu elektrycznym). 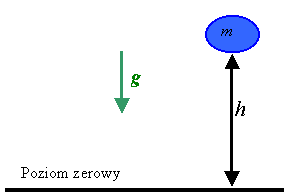Najprostszą postać energii potencjalnej otrzymujemy dla energii potencjalnej ciężkości ciał znajdujących się przy powierzchni ziemi. Wtedy wyraża się ona wzorem: Epot_ciezk = m · g · h Tutaj: |
Powyższy wzór można potraktować jako wniosek z zależności podanej
w rozdziale poprzednim. Napisano
tam o energii potencjalnej:
Ale przecież Fciężkości = m · g a droga S, to po prostu wysokość h. Po podstawieniu dostaniemy: Epot_ciezk = m · g · h |
Uwaga: |
