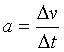Przyspieszenie

Wyprowadzenie wzoru na prędkość w ruchu jednostajnie zmiennym

Dane i założenia

Załóżmy, że mamy dane:

	prędkość ciała w pewnym momencie (czyli prędkość początkową v_p)
	przyspieszenie (a) jest stałe

Chcemy obliczyć jaką prędkość końcową (v_k), będzie miało to ciało po pewnym czasie t (zakładamy, iż czas ten też mamy dany).

Tak więc mamy

Dane:

v_p. a, t

Szukamy:

v_k

Przekształcenia

W celu obliczenia prędkości końcowej w ruchu jednostajnie zmiennym wykorzystamy wzór definiujący przyspieszenie (ew. patrz definicja przyspieszenia):

Aby z tego wzoru wyliczyć różnicę prędkości pomnożymy go obustronnie przez ∆t.

Otrzymamy wtedy wzór na "delta v", czyli przyrost prędkości:

∆v = a ∙ ∆t

Ponieważ jednak ∆v = v_k - v_p, więc

v_k - v_p = a ∙ ∆t

A stąd, po przeniesieniu prędkości początkowej v_pna drugą stronę równania (dodaniu do obu stron równania v_p):

v_k = v_p + a ∙ ∆t

Jaki wniosek można wyciągnąć z tego wzoru?

- w ruchu jednostajnie przyspieszonym prędkość przyrasta co sekundę o tę samą ilość metrów na sekundę
- np. jeśli początkowo prędkość wynosiła 6 m/s, a przyspieszenie ma wartość 3 m/s², to po pierwszej sekundzie prędkość wyniesie 9 m/s, po następnej 12 m/s, dalej 15 m/s, 18 m/s itd...

W ruchu jednostajnie opóźnionym będzie podobnie, ale ponieważ przyspieszenie ma przeciwny znak niż prędkość początkowa, to prędkość będzie malała

Np. jeśli początkowo prędkość ciała wynosiła 20 m/s, a ruch jest opóźniony z opóźnieniem o wartości 2 m/s², to po pierwszej sekundzie prędkość zmaleje do 18 m/s, po następnej do 16 m/s, dalej 14 m/s, 12 m/s itd...

Przykłady zastosowania wyprowadzonego wzoru są w rozdziale: Wzór na prędkość końcową w ruchu jednostajnie zmiennym.