Przyspieszenie

Przyspieszenie w ruchu krzywoliniowym

Przyspieszenie w ruchu prostoliniowym, a krzywoliniowym

W ruchu prostoliniowym przyspieszenie ma kierunek (ale niekoniecznie zwrot) zgodny z kierunkiem prędkości. Poza tym pełni ono tylko jedną rolę – wpływa na zmiany wartości prędkości. konkretniej - przyspieszenie wywołuje wzrost, lub malenie prędkości.

W przypadku ruchu krzywoliniowego sytuacja jest bardziej skomplikowana. Tutaj dochodzi jeszcze dla przyspieszenia pojawia się jeszcze jedna rola: zmiana kierunku prędkości (a więc także kierunku ruchu ciała).

Przyspieszenie w ruchu krzywoliniowym

W ruchu krzywoliniowym przyspieszenie jest skierowane pod kątem do prędkości.

Warto też zwrócić uwagę na fakt, że wektor przyspieszenia jest skierowany do wewnątrz łuku, po którym porusza się obiekt.

W celu wyjaśnienia jaką rolę pełni przyspieszenie w tym przypadku należy rozłożyć je na dwie składowe:

	Składową równoległą do prędkości (czyli styczną do toru i równoległą do kierunku ruchu), nazywaną też składową styczną: a_\|\|
	Składową prostopadłą do prędkości (prostopadłą do kierunku ruchu), nazywaną często składową normalną: a_n

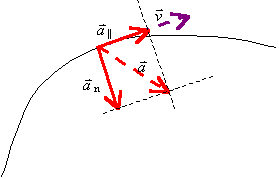
Te składowe pełnią dwie oddzielne role:

	Składowa równoległa a_\|\| odpowiada za zmianę wartości prędkości.
	Składowa prostopadła a_n odpowiada za zmianę kierunku prędkości.

Wartość składowej równoległej

Aby obliczyć wartość składowej równoległej (nazywanej też „składową styczną do toru”), wystarczy zastosować standardowy wzór na definicję przyspieszenia:

v – wartość prędkości – w układzie SI w m/s
t – czas – w układzie SI w s

Warto zwrócić uwagę na fakt, że v jest tu samą wartością prędkości, czyli nawet jeżeli prędkość zmienia kierunek, ale jej wartość się nie zmienia, to przyspieszenie styczne wynosi zero.

Wartość składowej prostopadłej

Aby obliczyć wartość składowej prostopadłej do kierunku ruchu, nazywanej też składową "normalną”, stosujemy wzór na przyspieszenie dośrodkowe (a_n = a_dosr):

v – wartość prędkości – w układzie SI w m/s
R – promień krzywizny toru – w układzie SI w metrach m

Warto znowu zwrócić uwagę na fakt, że v także jest tu samą wartością prędkości.

Więcej informacji na temat wzoru i składowej normalnej można znaleźć w rozdziałach poświęconych ruchowi po okręgu.

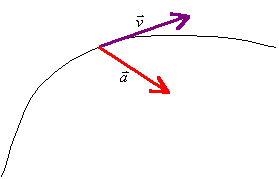Wektor przyspieszenia < Przyspieszenie w ruchu krzywoliniowym >