Orbity kołowe, a orbity eliptyczne
 Jak to napisano w rozdziale poświęconym
orbitom kołowym, aby tor
orbity miał dokładnie kształt okręgu, wartość siły
grawitacji musi zrównać się z siłą dośrodkową potrzebną
do utrzymania ciała na orbicie:
Fgraw = Fdośr
Jeśli to równanie nie zostanie zachowane,
otrzymamy orbitę inną niż kołową - najczęściej eliptyczną.
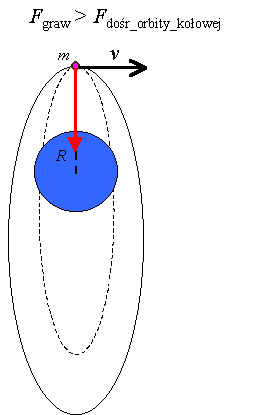
Np. dla siły grawitacji większej niż wystarczającej
do utrzymania ciała na orbicie kołowej
Fgraw >
Fdośr_orbity_kołowej
zakrzywienie orbity będzie silniejsze.
Dla dla takiej siły (większej niż siła dośrodkowa,
dla zadanej prędkości i promienia), otrzymamy nie ruch po okręgu,
lecz po elipsie.
Przy odpowiednim wydłużeniu tej elipsy tor ciał może nawet zawadzić
o powierzchnię Ziemi...
Z kolei gdyby siła grawitacyjna była mniejsza niż
siła dośrodkowa potrzebna do utrzymania ciała na orbicie kołowej,
wtedy ciało będzie miało skłonność do oddalania się od planety i
otrzymalibyśmy (w zależności od wartości prędkości) następujące
krzywe:
 | długą
elipsę (na rysunku jak powyżej byłaby ona płaska), gdy prędkość nie jest
jeszcze zbyt duża. |
| hiperbolę
w granicznym przypadku prędkości (v jest równe tzw.
drugiej prędkości kosmicznej liczonej dla promienia orbity) - ten
przypadek ma związek z tzw. drugą prędkością kosmiczną, choć
istotny jest tu jeszcze początkowy kierunek prędkości. W tym
przypadku ciało będzie oddalać się od planety coraz wolniej, aż
do nieskończoności, gdzie "teoretycznie" powinno się
zatrzymać. |
| parabolę
dla jeszcze większych prędkości (w tym przypadku ciało odleci od
planety do nieskończoności i już do niej nie wróci). |
Uwaga:
Elipsa,
parabola i hiperbola nazywane są niekiedy „krzywymi stożkowymi”,
ponieważ można je uzyskać w wyniku przecięcia stożka płaszczyzną.
|