Fale:

Fale - wstęp

Fala harmoniczna
Polaryzacja

Równanie fali

Prędkość fali

Długość fali, częstotliwość

	długość fali  λ
	okres fali T, lub częstotliwość fali f

Długość fali

Długość fali widoczna jest najlepiej wtedy, gdy na chwilę "zatrzymamy" falę w jej ruchu - sfotografujemy ją.

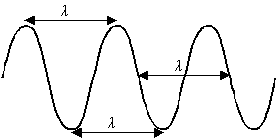
Wtedy długością będzie najmniejsza odległość między dwoma punktami fali, różniącymi się o dokładnie jeden cykl tych drgań - np. pomiędzy dwoma najbliższymi szczytami fali, ew. "dołami" fali. Może to być też odległość między punktami, które akurat nie ulegają w danej chwili wychyleniu. 

Przykład 
- "sfotografowana fala dźwiękowa" (proporcje są tu przesadzone, dla lepszej czytelności schematu).

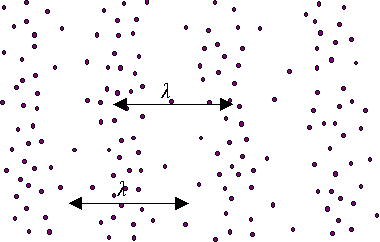
Długość fali to odległość między dwoma najbliższymi zgęszczeniami, lub rozrzedzeniami.

Okres fali

Okres fali jest wielkością, którą najlepiej widać, gdy skupimy się na drganiu jednego konkretnego punktu ośrodka. Na rysunku niżej czerwony koralik jest pobudzany przez falę do drgań  góra - dół. Okres tych drgań wynosi 1,5 s, co oznacza, że czas, po jakim koralik wykona jedno pełne drganie wynosi właśnie 1,5 s.

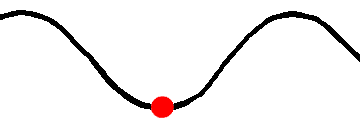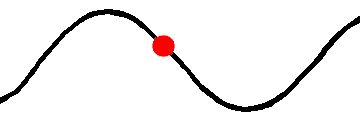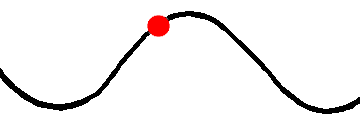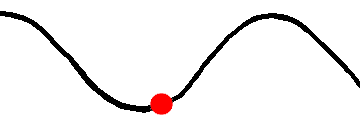
Co to jest jedno pełne drganie?

Pełne drganie otrzymamy np. gdy:

	koralik będący początkowo w maksymalnym górnym położeniu zejdzie maksymalnie w dół, a następnie powróci do maksymalnego górnego położenia
	koralik będący początkowo w maksymalnym dolnym położeniu wzniesie się maksymalnie w górę, a następnie powróci do maksymalnego dolnego położenia
	koralik znajdujący się na poziomie 0 (pośrodku między maksymalnymi położeniami) odbędzie jedno pełne wychylenie w górę, wróci do położenia 0, a następnie wykona wahnięcie w dół i znowu wróci do położenia 0.
	ogólnie - gdy koralik "odwiedzi" wszystkie swoje położenia jakie występują podczas drgania i znajdzie się dokładnie w tym samym punkcie.

Warto zapamiętać:

Okresem fali nazywamy czas, w którym punkt ośrodka wykonuje jedno pełne drganie.

Okres drgań wyrażamy w sekundach. 

Częstotliwość drgań fali

Częstotliwość drgań jest ściśle związana z okresem. 

Częstotliwość równa jest ilości drgań, jakie wykonują punkty ośrodka w ciągu jednostki czasu (najczęściej 1s).

Częstotliwość jest odwrotnością okresu:

Czyli w naszym przypadku, gdy okres drgań koralika wynosił 1,5 s, częstotliwość wyniesie:

f = 1/1,5 = 2/3 

Częstotliwość drgań koralika (a także częstotliwość fali pobudzającej koralik do drgań) wynosi 2/3 Hz (ok. 0,67 Hz).

Fale - wstęp << Długość fali, częstotliwość >> Polaryzacja