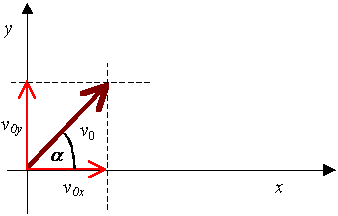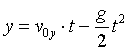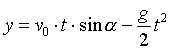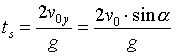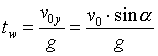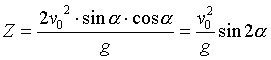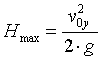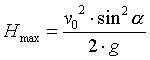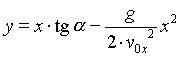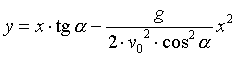|
|
Rzut ukośny
Opis ruchu
W rzucie ukośnym mamy do czynienia z lotem ciała
wyrzuconego z poziomu zerowego (y0 = 0). Ciału jest
nadawana prędkość o wartości v0, skierowana pod kątem
α do poziomu. Ciało porusza się łukiem, by po pewnym czasie opaść
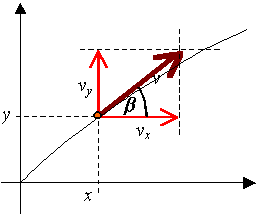
na ziemię. Wygodnie jest umieścić rysunek rzutu ukośnego w układzie
współrzędnych, co ułatwia orientację w nazwach zmiennych i pozwala
na wyprowadzenie równania toru.
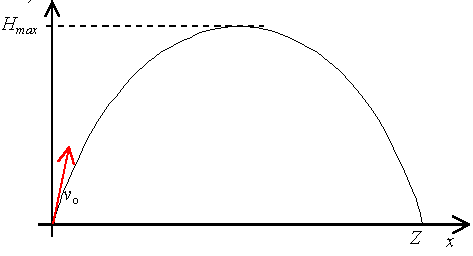
Odległość jaką przebywa ciało w poziomie do momentu upadku na
poziom początkowy nazwiemy zasięgiem (Z) rzutu ukośnego.
| Początkowe położenie: |
x = 0
y = 0 |
| Kąt, jaki prędkość początkowa
tworzy z poziomem: |
α |
| Prędkość początkowa ma wartość
v0 |
Prędkość pocz. pozioma: v0x
= v0 · cos α
Prędkość pocz. pionowa: v0y = v0
· sin α |
| Przyspieszenie ma wartość
g. |
Przyspieszenie w tym ruchu jest stałe i
jest skierowane pionowo w dół. |
W przypadku gdy nie musimy uwzględniać
oporu powietrza, torem ruchu ciała jest parabola. Ruch ciała rozkłada
się wtedy na dwa ruchy prostsze:
 | ruch w poziomie (współrzędna X-owa) – odbywa się ze stałą
prędkością o wartości składowej poziomej prędkości początkowej
v0X |
 | ruch w pionie (współrzędna Y-owa) – jest w istocie rzutem
pionowym, czyli ruchem jednostajnie zmiennym z prędkością początkową
równą składowej pionowej v0Y. |
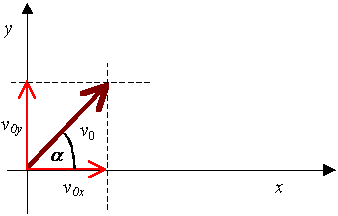
Wzory opisujące rzut ukośny
vx = v0x = const
vx = v0·cos α
vy = v0·sin α - g·t
Odległość pozioma przebyta w poziomie po czasie t:
x = vox ·t = v0·t·cos
α
Wysokość na jakiej znajduje się ciało po czasie t:
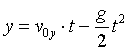
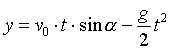
Czas lotu do momentu upadku na poziom początkowy:
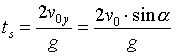
Czas wznoszenia do osiągnięcia maksymalnej wysokości:
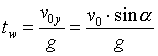
tw = ½ ts
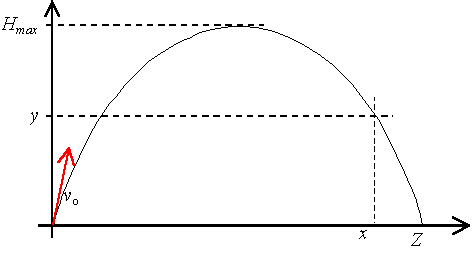
Tor rzutu ukośnego ma kształt paraboli
skierowanej ramionami w dół
Równanie toru rzutu ukośnego
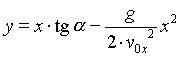
lub
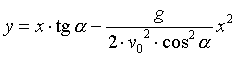
|