| wielkość |
wzór |
co we wzorze |
|
Drgania harmoniczne |
| okres drgań wahadła matematycznego |
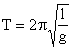 |
l - długość wahadła w metrach
g - przyspieszenie grawitacyjne (ziemskie) w m/s2 |
| Równanie ruchu harmonicznego |
a = – ω2x

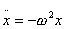 |
x
– wychylenie
a – przyspieszenie ruchu
v – prędkość ruchu
f – częstotliwość,
T - okres drgań (fali)
A, B – amplituda
φ – faza początkowa
ω - częstość kołowa,
ω = 2 π f = 2 π / T
tutaj k - stała sprężystości sprężyny, lub innego
układu odpowiedzialnego za powrót do położenia równowagi.
k = – ω2m
|
| Wychylenie w ruchu harmonicznym |
x = A cos ω t
x = A sin ω t+ B sin
ω t
x = A sin (ω t + φ
) |
| Prędkość w ruchu harmonicznym |
v = A ω cos (ω t + j
) |
| Przyspieszenie w ruchu harmonicznym |
a = – A ω2 sin
(ω t + φ ) |
| Energia potencjalna w ruchu harmonicznym |
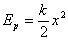 |
|

Drgania tłumione |
| Równanie różniczkowe drgań tłumionych |
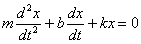 |
|
| Rozwiązanie równania różniczkowego - równanie
ruchu drgań tłumionych |
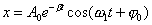
Amplituda drgań tłumionych:
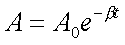 |
Gdzie:
ω - częstość kołowa drgań bez tłumienia
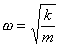
częstość kołowa drgań tłumionych:
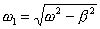
współczynnik tłumienia:
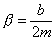
|
| Logarytmiczny dekrement tłumienia |
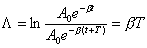 |
Logarytm z ilorazu „amplitudy” (chwilowej) w
stosunku do „amplitudy” po czasie równym okresowi
drgań.
Słuszne, gdy ω > β (ω1
- istnieje jako liczba rzeczywista)
|