Bilans cieplny – przykład rachunkowy

Oto przykład praktycznego wykorzystania zasady bilansu cieplnego.
Rozwiążmy następujący problem:

Zadanie

Kowal zanurza do kadzi z 6 l wody rozgrzany stalowy pręt, w wyniku czego, w krótkim czasie temperatura wody wzrasta od 20°C do 70°C. Masa pręta wynosi 2 kg. Jaką temperaturę miał pręt przed zanurzeniem?

Rozwiązanie

W opisanej sytuacji mamy do czynienia z przekazywaniem ciepła od pręta do wody. Temperatury pręta i wody - początkowo różne – po wymianie ciepła będą miały jedną temperaturę końcową (oznaczymy ją przez t_k). Temperatura ta będzie większa od początkowej temperatury wody, ale mniejsza od początkowej temperatury pręta.
Zastosujemy tu bilans cieplny – w tej konkretnej sytuacji będzie on miał postać:

Q_{pobrane_przez_wodę} = Q_{oddane_przez_pręt}

Zarówno ciepło pobrane, jak i oddane będzie wyliczane ze wzoru na ciepło ogrzewania bez zmiany stanu skupienia:

Q = m·c_w·Dt

Różne będą jednak substancje i różnice temperatur:

Q_{pobrane_przez_wodę} = m_wody ·c_{w_wody}· (t_k – t_{p_wody})

Q_{oddane_przez_pręt} = m_pręta ·c_{w_stali} · (t_{p_pręta} – t_k)

Dane tu są:

m_wody = 6 kg (bo litr wody waży 1 kg)
m_pręta = 2 kg
c_{w_stali} = 500 J/kg°C (dana odczytana z tablic)
c_{w_wody} = 4200 J/kg°C (dana odczytana z tablic)
t_k = 70°C
t_{p_wody} = 20°C

Szukamy

t_{p_pręta} = ?

Przekształcenia

Podstawiamy wyrażenia na ciepło pobrane i oddane do równania bilansu cieplnego:

m_wody ·c_{w_wody}· (t_k – t_{p_wody}) = m_pręta ·c_{w_stali} · (t_{p_pręta} – t_k)

W powyższym równaniu wszystko jest dane z wyjątkiem t_{p_pręta}.

Dzielimy obie strony równania przez: m_pręta ·c_{w_stali}, a następnie dodajemy do obu stron równania t_k. Ostatecznie otrzymamy wtedy wzór na szukane t_{p_pręta}:

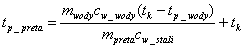
Po podstawieniu liczb otrzymamy wynik końcowy:

t_{p_pręta}= 1330°C.