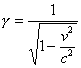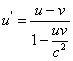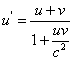Wzory teorii względności

Oznaczenia i symbole

Prędkość światła: c =  299792458 m/s

Prędkość obiektu względem układu odniesienia: v.

Czynnik  γ - czynnik Lorentza (występuje w wielu wzorach teorii względności).

Wartości  γ :

	v = 0 → γ = 1
	v < c  → γ > 1
	v = c  → γ  rośnie do nieskończoności

Czynnik β - stosunek prędkości obiektu (obserwatora) do prędkości światła:

Dla

	v = 0 → β = 0
	v < c → β <1
	v = c → β = 1

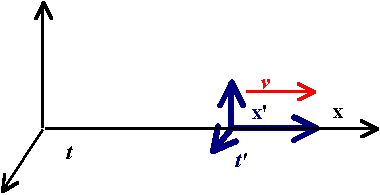
Transformacja Lorentza

Ustalenia początkowe:

Rozpatrujemy dwa inercjalne układy odniesienia – zwykły XYZ i oznaczany ‘ (primem) X’Y’Z’. Oba układy mają równolegle położone osie X Y Z. W chwili początkowej środki obu układów pokrywają się – czyli:

x (t = 0) = x’(t’= 0) = 0

y (t = 0) = y’(t’= 0) = 0

z (t = 0) = z’(t’= 0) = 0

Prędkość układu primowanego względem układu nieprimowanego wynosi v i jest skierowana wzdłuż osi X-ów zgodnie z jej zwrotem.

Wzory transformacyjne

Oto wartości poszczególnych współrzędnych dla zdarzenia mającego w układzie nieprimowanym współrzędne: x, y, z, t:

z' = z

y' = y

x' = γ ( x – vt )

t' = γ ( t – x β/c )

Wzory transformacyjne - transformacja odwrotna:

z = 'z

y = y'

x = γ ( x’ + v t’ )

t = γ ( t’ + x’ β/c )

Relatywistyczna transformacja prędkości

Załóżmy, że mamy cząstkę, której prędkość w układzie nieprimowanym dana jest przez u. Prędkość względna układów wynosi (jak w transformacji Lorentza) v.

u = (u_x, u_y, u_z)

W układzie primowanym prędkość tej cząstki będzie widziana jako:

u' = (u’_x, u’_y, u’_z)

Przy czym zachodzi:

Przypadek jednowymiarowy – dodawanie i odejmowanie prędkości w jednym wymiarze

Aby wzór łatwiej się oglądało pozbywamy się indeksu oznaczającego współrzędną.

Wzór na u’ w postaci rozpisanej:

Co można uznać za wzór na relatywistyczne odejmowanie prędkości (czyli gdy obiekty, a zarazem układy odniesienia, poruszają się w tym samym kierunku).

Wersja dla obiektów/układów odniesienia poruszających się w przeciwnych kierunkach (relatywistyczne dodawanie prędkości ) będzie różnić się znakiem prędkości u.

Wnioski – po podstawieniu do wzorów otrzymamy:

1. dla dowolnych u < c oraz v ≤  c zachodzi u’< c
2. dla u = c i v = c, u’=c.

Dylatacja czasu

Oznaczmy czas własny układu przez t₀ - jest to czas upływający pomiędzy dwoma zdarzeniami w układzie w którym zdarzenia zachodzą w tym samym miejscu. Czas t' mierzony pomiędzy tymi zdarzeniami w układzie poruszającym się dany będzie wzorem

t' = t₀ /γ

Jest to efekt tzw. dylatacji (wydłużenia czasu), ponieważ γ ≥ 1, więc

 t₀ ≥ t'

Oznacza to, że w układzie primowanym upływa mniej minut, a więc czas się wydłuża.

Skrócenie długości

Niech długość pewnego odcinka w układzie, w którym spoczywającym względem tego odcinka wynosi l₀. Długości tego odcinka obserwowane z układu ruchomego  skracają się γ krotnie.

 l_{obserwowane_w_ruchu}=l₀/γ

ponieważ γ ≥ 1, więc l_{obserwowane_w_ruchu} ≤ l

Oznacza to, że odcinek poruszający się wraz z obserwatorem jest γ razy dłuższy

Zjawisko powyższe nazywane jest niekiedy kontrakcją długości lub skróceniem Lorentza – Fitzgerlada.

Interwał czasoprzestrzenny

Np. wzór tzw. interwału czasoprzestrzennego.

W postaci symetrycznej względem wszystkich współrzędnych
∆s² = - (∆x)² – (∆y)² – (∆z)² - (ic∆t)².

Lub prościej (choć nie tak elegancko matematycznie), bo bez użycia jednostki urojonej i. :

∆s² = (c∆t)² - (∆x)² – (∆y)² – (∆z)²