Zadania niebagatelne

Zadania niebagatelne, to taki rozdział z zadaniami szczególnymi. Najczęściej będą one trudne. Mało tego często będą postawione w sposób dość przewrotny. To zadania dla prawdziwych zadaniowych "twardzieli". Niektóre są znane, inne może nie (autor wymyśla je sobie sam, ale pewnie się powtarzają, jako że fizyka jest jedna i ograniczona w typowych szkolnych zastosowaniach). Zadania będą opatrzone tytułami, nawias obok pokazuje stopień trudności zadania (na jaką ocenę szkolną jest wyceniane przez autora).

Te zadania mają jeszcze jedną zaletę - coś uświadamiają, coś tłumaczą w zjawiskach życia codziennego, a nie są tylko sztuką dla sztuki rozwiązywania zadań.

Kinematyka i dynamika

To poniższe zadanie wiąże się z typowym problemem szybkości pojazdów na dłuższych i krótszych odcinkach. uświadamia ono lepiej istotę prędkości średniej.

Prędkość średnia na krótszych i dłuższych odcinkach(6)
Metro przejeżdża przystanek o długości 1km ze średnią prędkością 50km/h, a odcinek o długości 1,5 km ze średnią prędkością 55km/h. Jaką średnią prędkość osiągnie to metro na odcinku 2km? 
Wskazówka: załóż, że nie zmieniają się parametry napędu, ani obciążenie wagoników metra, zaś cała różnica w prędkościach wynika ze stosunku czasu jazdy z maksymalną prędkością wobec odcinków przyspieszania i hamowania (cały odcinek składa się z trzech etapów – rozpędzanie, ruch jednostajny, hamowanie i tylko ten środkowy etap różnicuje średnią prędkość ruchu na całym odcinku). Dla uproszczenia załóż także, że zarówno podczas hamowania, jak i przyspieszania ruch jest jednostajnie zmienny.

Odp. V3  = 1100/19 ≈ 57,9

Wzory: 

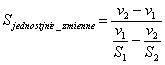
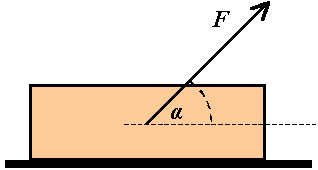
Jak przesuwać ciała?

 {6} Ciało o masie m leży na poziomej powierzchni Współczynnik tarcia statycznego ciała o powierzchnię wynosi f. Jakiej minimalnej siły trzeba użyć (i pod jakim kątem nią działać), aby ruszyć ciało z miejsca?
Podać maksymalne przyspieszenie klocka pod działaniem danej siły F.

 

Odp.

odp. kąt siły działającej optymalnie tg α = f, 
Wartość minimalna siły potrzebnej do ruszenia ciała: Fmin = fmg/ √(1 + f2),
Przyspieszenie (dla F > Fmin,  bo dla F ≤ Fmin, a = 0),

 

 

Wnioski:
W przypadku braku tarcia, najefektywniej jest ciągnąć ciało poziomo.
Im większy jest współczynnik tarcia, tym bardziej "opłaca się" ciągnąć ciało pod kątem - do góry. Jednak opłacalność ta jest tylko do pewnego kąta - wyznaczonego zależnością:  tg α = f.