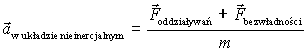Wstęp |
|||||||||||||||||||||||||||||||||||||||||||
Autor tego opracowania przez wiele lat
W pewnym momencie przychodzi pora na refleksje. Cóż
wiem, że błędy być muszą, ale trzeba je też poprawiać. Najważniejszym moim celem i życzeniem nie jest przytaknięcie mi, czy np. "oklaski uznania", lecz to, że ktoś zrozumie dlaczego. Może wtedy okazać się, że wiele problemów dydaktycznych (szczególnie przy rozwiązywaniu zadań), które do tej pory trudno było pokonać, "rozwiązuje się samo" tylko dzięki zmianie sposobu ujęcia.
|
|||||||||||||||||||||||||||||||||||||||||||
KinematykaBzdura nr 1, czyli sprawdzanie wzorów matematycznych, czyli badanie ruchu jednostajnegoInteresującym przykładem bezsensu w nauczaniu
fizyki w szkole jest podręcznikowo - programowe doświadczenie pod tytułem
"badanie ruchu jednostajnego". Jaki jest sens "sprawdzania" definicji?... Mówiąc inaczej - najpierw zakładamy, że nasz ruch jest jednostajny - a potem to "udowadniamy"... Czy można powyższy temat zrealizować sensownie? - oczywiście, jednak trzeba przyjąć najpierw definicję prędkości (bez sprawdzania, bo to jest definicja), a potem można np. badać czy (!!!) rzeczywisty ruch jest jednostajny. Mówiąc inaczej sprawdzamy, czy:
- jeśli tak - to ruch jest jednostajny, jeśli nie - to nie. Ale nie możemy najpierw czegoś założyć, a potem tego założenia udowadniać; możemy co najwyżej przypuszczać to czy tamto i sprawdzać to. Przy okazji (bardzo ważny metodologicznie element) musimy założyć np., że odchylenie 5% ustalamy za akceptowalne, bo inaczej trudno nam będzie wyciągać ostateczny wniosek dotyczący ruchu. Sprawdzamy więc np. czy:
Innym przykładem powyższej bzdury jest udowadnianie, że w ruchu jednostajnie przyspieszonym (np. na równi) droga rośnie proporcjonalnie do kwadratu czasu - przecież to jest założenie!!! (pośrednio - jako ścisły matematyczny wniosek z definicji ruchu jednostajnie przyspieszonego)! Można natomiast badać:
- a to byłoby sensowne i wartościowe doświadczenie.
|
|||||||||||||||||||||||||||||||||||||||||||
Prędkość czy przyspieszenie? - czy uda się wreszcie tego nauczyć?...Podstawowym błędem popełnianym przez uczniów podczas nauki kinematyki jest mylenie prędkości z przyspieszeniem. Wynika to z faktu, że w istocie wielu uczniów nie rozróżnia tych wielkości. Dla przekonania się proponuję zrobić test (pisemny bądź ustny): 1. Z tego że przyspieszenie ciała wynosi zero wynika, że
2. Przyspieszenie hamującego samochodu
3. Ciało rzucone do góry ma podczas wznoszenia przyspieszenie
4. Przyspieszenie ciała poruszającego się ruchem prostoliniowym
Dlatego dobrze jest uświadomić uczniom, że przyspieszenie jest to jakby "siła" ciągnąca koniec wektora prędkości, a nie samo ciało. - jeśli ciągnie prędkość zgodnie z jej zwrotem - to ją wydłuża
|
|||||||||||||||||||||||||||||||||||||||||||
Ruch przyspieszony, a ruch opóźnionyCzęstym błędem w nauczaniu kinematyki jest podawanie, że wzór
ma dwie postacie:
Podobnie wersjonuje się (przepraszam za ten nie do końca elegancki wyraz) wzór na drogę:
Takie mnożenie wzorów powoduje w konsekwencji duże kłopoty interpretacyjne (wyjaśniam dalej), obciążenie pamięci, niespójność z różnymi "uznanymi" wzorami i ogólny zamęt myślowy. Faktem jest, że opisywana błędna interpretacja wzorów jest polecana także w kilku podręcznikach do fizyki zatwierdzonych przez MEN (na szczęście nie wszystkich, bo są i takie, gdzie sprawa jest dobrze tłumaczona - np. w podręczniku Macieja Jenike). Jednak chwila zastanowienia nad problemem prowadzi do nieuchronnego wniosku, że stosowanie dwóch postaci wzorów nie ma żadnego sensownego uzasadnienia. Jak jest dobrze w tym przypadku?Uważam, że zdecydowanie lepiej jest stosować inną konwencję, a mianowicie: - ogólne wzory słuszne są tylko w wersji z plusami:
Ale Dlaczego lepiej jest podawać tylko jedną postać wzorów? Odpowiedzią jest taki przykład - zadanie:
Rozwiązanie: v = 6 + 5 ∙t oraz Ruch opóźniony: v = 6 - 5 ∙t oraz Według interpretacji "dwuwzorowej" - otrzymujemy po prostu błędne wyniki i właściwie nie ma jak tego wytłumaczyć (poza stwierdzeniem, że opisana interpretacja jest błędna). Zadanie 2Ciało rzucono pionowo do góry z prędkością początkową 10 m/s. Rozwiązanie polecane przez mnie (interpretacja jednowzorowa)- konwencja: kierunek dodatni - do góry Przyjmujemy dane: Vo= 10 m/s, a = - g = - 10m/s2. vkońc = vpocz + a ∙
t oraz vkońc = 10 - 10 ∙ 1,5 = -5
Odp. Prędkość końcowa wyniesie 5 m/s i będzie skierowana w w dół (ciało już spada - bo jest minus przy wartości Vkońc), wysokość ciała w tym momencie wyniesie ok. 3,8 m. KONIEC. Rozwiązywanie metodą dwóch wersji wzoruSzkic rozwiązania metodą nie polecaną przez mnie, czyli przy założeniu, że ruchem przyspieszonym rządzi wzór z plusem, a opóźniony z minusem (ta metoda jest zbyt długa i żmudna, żeby mi się chciało robić ją, a w szczególności opisywać tu w całości):
Tak szacunkowo daje to około 5 razy więcej roboty (a więc także możliwości pomyłki). To zadanie naprawdę nie jest wyjątkiem - dla większości zadań z ruchem przyspieszonym łatwiej jest stosować konwencję jednej postaci wzorów! Podsumowując pozostałe argumenty za "jednowzorowym" ujęciem, mamy:
Czy jest jakaś wada? Właściwie jedna - trzeba dodatkowo nauczyć się konwencji znaku. Mówiąc inaczej nauczyciel powinien poświęcić z jedną lekcję na wytłumaczenie kiedy rzut wektora na wybraną oś da wartość dodatnią, a kiedy ujemną. To jest dodatkowa robota, ale też i potrzebna, a nawet niezbędna, bo bez jej wykonania problemy z kinematyką będą się ciągnąć często przez całą szkołę średnią. |
|||||||||||||||||||||||||||||||||||||||||||
DynamikaZwiązek między pierwszą i drugą zasadą dynamiki - często spotykane błędy świadczące o niezrozumieniu mechaniki newtonowskiejTypowe szkolne podejście do pierwszej zasady dynamiki przedstawia się tak. Pierwsza zasada dynamiki:
Druga zasada dynamiki:
Stąd wynika często stosowany wzór (nazywany też właśnie II zasadą dynamiki, choć ja raczej nazwałbym definicją siły opartą o przyspieszenie):
Wnioski, jakie można wyciągnąć z takiego przedstawienia zasad dynamiki:
A stąd kolejny, ale już idiotyczny wniosek:
(tak z resztą napisano w podręczniku "Fizyka" Holliday
Resnick... - cóż nawet autorytety popełniają błędy). Rozwiązanie problemu - co jest do czego i po co... Jak to jest więc z I i II zasadą dynamiki?Pierwsza zasada dynamiki jest bardzo potrzebna, ponieważ ustanawia warunki w których będzie obowiązywała (gdy ją zaraz wprowadzimy) druga zasada dynamiki. Do tego potrzebne jest jednak pojęcie układu inercjalnego. Układ inercjalny jest to taki układ, w którym spełniona jest... pierwsza zasada dynamiki (...?) - ze sformułowania szkolnego:
Od razu pojawia się pytanie: a jak bez sił mogłoby
w ogóle być przyspieszenie? Nowe sformułowanie pierwszej zasady dynamiki to:
Tak właśnie! - mamy od czego zacząć! Teraz przynajmniej w jednej klasie układów wiemy (w naszym, dobrze wybranym, układzie inercjalnym), że gdy nie ma sił, to nie ma przyspieszenia. Jest więc sens zastanawiać się dalej:
Bo w innym przypadku zarejestrowane przyspieszenie może być wywołane wyłącznie ruchem układu odniesienia, a nie będzie detektorem siły. Tak więc tylko w układach inercjalnych: obowiązuje Uwaga: tutaj zamiast zwykłego F napisałem specjalnie Foddziaływań, aby podkreślić fakt, że "prawdziwe" siły są efektem oddziaływania i tylko dla nich obowiązuje "normalna" 2 zasada dynamiki. Za chwilę jednak powiemy o możliwości wprowadzenie takich "pseudo-sił", które rozszerzą zakres stosowania tego II zasady dynamiki. A w układach nieinercjalnych?
Można jednak poprawić opis układów nieinercjalnych tak, aby obowiązywała w nich zmodyfikowana wersja II zasady dynamiki. W tym celu do rzeczywistych sił (a więc sił wynikających z oddziaływań) trzeba dodać sztuczną pseudo-siłę (siłę nie biorącą się z żadnego oddziaływania, lecz wynikającą z ruchu układu odniesienia). Ta sztuczna siła (właściwie nie siła tylko "poprawka" do sił) równoważy wpływ dodatkowego przyspieszenia związanego z układem odniesienia i nazywa się siłą bezwładności. Siła ta jest równa: A oto treść zmodyfikowanej II zasady dynamiki (z poprawką na nieinercjalność układu):
I ta poprawiona wersja II zasady dynamiki Newtona dopiero teraz dobrze działa w układach nieinercjalnych.
|
|||||||||||||||||||||||||||||||||||||||||||
|
Następny problem: siłę obliczamy znając przyspieszenia, przyspieszenie jest wynikiem siły, masę obliczamy dzięki działaniu siły (znowu) ciężkości lub sprężystości - masło maślane, lub co jest pierwsze jajko, czy kura...? |
 |
||||||||||||||||||||||||||||||||||||||||||
|
Tu odpowiedź jest znacznie mniej
jednoznaczna. Bo właściwie nie mamy gwarancji, czy my, Układ
Słoneczny (a nawet cała supergromada galaktyk) nie podlegamy
działaniu jakiejś kosmicznej supersiły ciągnącej to
zbiorowisko w jednym kierunku.
Jak na razie nasze poznawanie sił ograniczamy więc do sfery lokalnej. Ustalamy po prostu, że po dołączeniu pewnego oddziaływania (stwarzamy warunki dla tego oddziaływania) do określonego ciała obserwujemy dodatkowe przyspieszenie. Następnie staramy się wyróżnić ów czynnik wywołujący przyspieszenie i powiązać jego wartość wartością dodatkowego przyspieszenia. Jeżeli to co ustaliliśmy na temat naszej siły potwierdza się zawsze w nowych warunkach, to możemy uogólnić nasze ustalenia dotyczące tej siły. A masa? Masę możemy wyznaczać niezależnie z zasady zachowania pędu. Np. zderzamy niesprężyście ciało o znanej masie m (np. wzorzec kilograma) z ciałem o nieznanej masie mx i wyliczamy to co trzeba ze wzoru:
Tak więc masę można wyznaczać niezależnie od pojęcia siły.
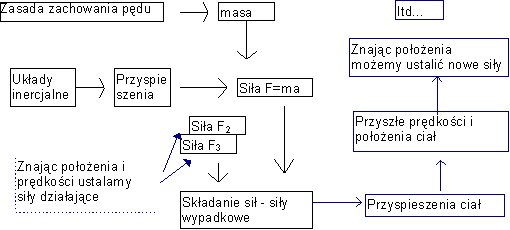
I tak właściwie, to nauczanie dynamiki powinno zaczynać się od zasady zachowania pędu, gdyż dzięki niej mamy możliwość wprowadzenia w miarę niezależnej od układu odniesienia (pomijam efekty relatywistyczne) definicji masy. Sensowny logicznie schemat nauczania dynamiki to:
Jak na razie robi się to odwrotnie - najpierw składanie sił, chociaż jeszcze nie wiadomo co to jest siła, potem niepełna, błędna wersja zasad dynamiki, a na koniec zasada zachowania pędu - ot tak, na dodatek... |
|||||||||||||||||||||||||||||||||||||||||||
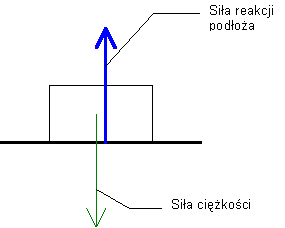
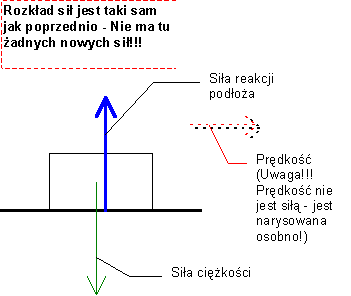
Rozkład sił działających na ciało - typowe i nagminne horrendalne (!!!) błędy robione nawet(!) przez nauczycieli i autorów podręczników do fizyki!Zadanie 1. Ciało spoczywające na poziomej powierzchniJakie siły działają na spoczywające na poziomej płaszczyźnie ciało? Rozwiązanie dobre (a nie rysuję tego złego, bo się jeszcze utrwali przez samo patrzenie...)
(właściwie, to obie strzałki wektorów powinny się częściowo pokrywać, ale wtedy słabiej wyłoby widać, że siła ciężkości wychodzi od środka ciała, a siła reakcji o środka obszaru styku między klockiem i podłożem. A teraz błędy, czyli co tu można jeszcze narysować (mijając się w ten sposób z fizyką)?
|
|||||||||||||||||||||||||||||||||||||||||||
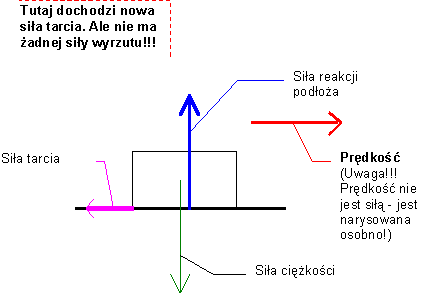
Zadanie 2 ciało sunące bez tarcia po poziomej płaszczyźnieJakie siły działają na ciało sunące bez tarcia ruchem jednostajnym po poziomej płaszczyźnie (np. w przybliżeniu bardzo śliski krążek hokejowy)?
3. Jakie siły działają na ciało sunące z tarciem (czyli poruszający się ruchem opóźnionym) po poziomej płaszczyźnie?
Ale co tu można zrobić błędnie?
Warto zwrócić uwagę na fakt, że tutaj siła wypadkowa jest skierowana przeciwnie do kierunku ruchu!
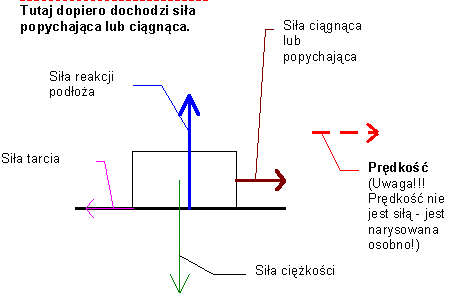
Zadanie 4 Ciało popychane lub ciągnioneI dopiero teraz przypadek ciała "popychanego" - np. szafy przesuwanej po podłodze. Tutaj dopiero działa siła w kierunku ruchu.
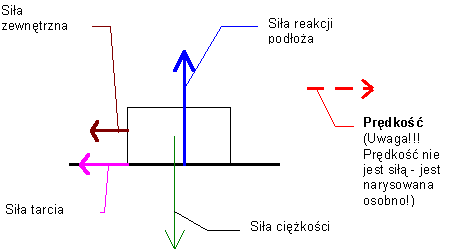
Ale ciekawy problem Jakiej sytuacji odpowiada powyższy rozkład sił (tutaj wszystkie poziome siły są przeciwne do prędkości)?
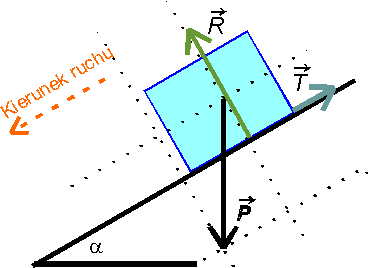
Zadanie 5. Rozkład sił na równiJakie siły działają na ciało zsuwające się z równi (z tarciem)? Na ciało zsuwające się z równi pod wpływem siły ciężkości działają trzy siły
Źródłem pierwszej siły jest planeta Ziemia, a źródłem dwóch pozostałych równia.
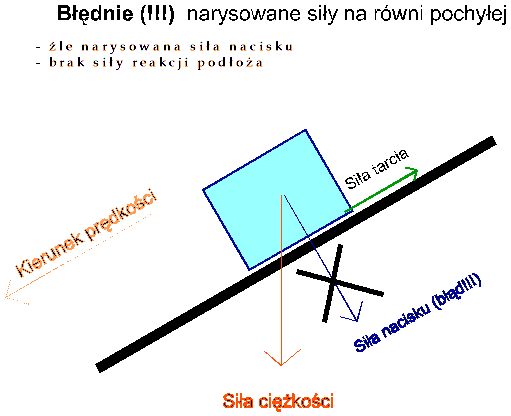
Jednak dość często spotyka się OKROPNY BŁĄD (popełniany nagminnie nawet przez nauczycieli, a czasami przez twórców podręczników) polegający na myleniu sił działających na ciało z siłami, którymi działa to ciało na otoczenie. A oto typowy błędny rozkład sił na równi:
Uwagi:Najczęściej spotykanym błędem popełnianym przy rozkładzie sił na równi jest rysowanie w dół siły nacisku. Błąd ten wynika najprawdopodobniej z tego, że oczywiste jest, że klocek naciska na równię i rysujący próbuje gdzieś tę siłę umieścić. Jednak: tak skierowana siła działa nie na klocek, lecz na równię! - my, przy obliczaniu przyspieszenia klocka, rozpatrujemy siły działające na klocek! siła działająca ze strony równi na klocek nie jest przyciągająca, lecz utrzymująca go aby nie opadł, a więc jest to siła dokładnie przeciwna do błędnie tu narysowanej siły nacisku. gdyby na klocek działały tylko takie siły (jak te narysowane, łącznie z przekreśloną), to powstawałaby z tego siła wypadkowa skierowana w dół, na prawo. W tym kierunku ciało powinno też nabierać prędkość i "drążyć" równię, a nie zsuwać się w dół na lewo. A gdzie w związku z tym jest siła nacisku? Trzeba tu rozróżnić dwa rodzaje nacisków:
Błąd jaki się tu często popełnia wynika zapewne z pewnych naleciałości psychologicznych - otóż najczęściej jako nacisk uważamy siłę działającą w dół - np. nacisk na podłogę, nacisk piramidy książek na klejony element itp... Jednak w rzeczywistości nacisk może być pod dowolnym kątem i w przypadku klocka na równi podtrzymuje on go (częściowo) przed spadaniem. Wyżej opisany błąd też występuje, niestety, w jednym (przynajmniej jednym, bo nie sprawdzałem wszystkich) z zaakceptowanych przez Ministerstwo Edukacji podręczników... |
|||||||||||||||||||||||||||||||||||||||||||