Odczytywanie i interpretowanie wzorów.Spis treści rozdziału: WstępPrawa fizyki są najczęściej zapisywane w postaci wzorów matematycznych. Dlatego niezbędną umiejętnością każdego fizyka, jest odczytywanie i zrozumienie zależności tak przedstawionych. Odczytywanie praw i wzorówIstnieją proste reguły, które pozwalają wzór matematyczny przetłumaczyć na "język mówiony", czyli inaczej mówiąc, poprawnie przeczytać. Przy odczytywaniu praw fizycznych, stosujemy następujące zasady:
|
| Przykład 1:
Prawo (II zasada dynamiki): czytamy: a jest wprost proporcjonalne do F i odwrotnie proporcjonalne do m. Przykład 2: Prawo "Ohma": czytamy: I jest wprost proporcjonalne do U i odwrotnie proporcjonalne do R. |
|

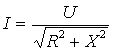 (nie zawiera stałych
fizycznych) można przeczytać na wiele sposobów w zależności od
potrzeb:
(nie zawiera stałych
fizycznych) można przeczytać na wiele sposobów w zależności od
potrzeb: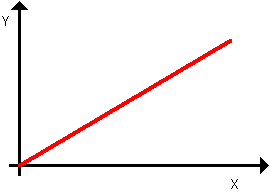
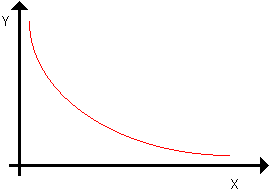
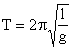 interpretacja zależności T od g jest następująca:
interpretacja zależności T od g jest następująca: